初级侧反饋控制 (PSR) 电源供应器的缆线补偿
Cable Compensation of a Primary-Side-Regulation (PSR) Power
Supply
摘要
缆线补偿是用来补偿缆线阻抗因电流流经而产生的电压降,以便提供电池充电器等应用一稳定充电电压的方法。本应用须知介绍一种新的、被称为缆线减法补偿
(cable minus compensation) 的补偿方法,并以之为例来说明在初级侧反饋控制
(PSR, Primary Side Regulation) 反激式转换器中缆线补偿的概念和设计方法,其分析结果也将藉电路仿真结果来进行验证。
1. 简介
初级侧反饋控制 (PSR,Primary Side Regulation) 的反激式转换器,因具有低成本与控制简易的优点,被广泛地应用于离线式电池充电器上。在初级侧反饋控制中,二次侧的输出电压是透过初级侧之辅助线圈
(auxiliary winding) 进行间接检测的,该检测信号再经由精确的侦测电路对输出进行控制可得到很好的稳压输出。然而,这些应用中的电子产品像手机或平板电脑等设备在充电时通常都会透过一条长缆线与电源转换器
(adapter) 连接,若适配器的输出为一个稳定的电压源,当输出电流流过缆线阻抗时,就会在缆线上形成电压降,连接负载的另一端电压则会相应变低。此降低的充电电压不仅可能会造成电池充电时间延长,甚至可能会无法符合充电电压的规格,这在低压大电流的充电应用上表现尤其严重。图一可用来说明此现象。
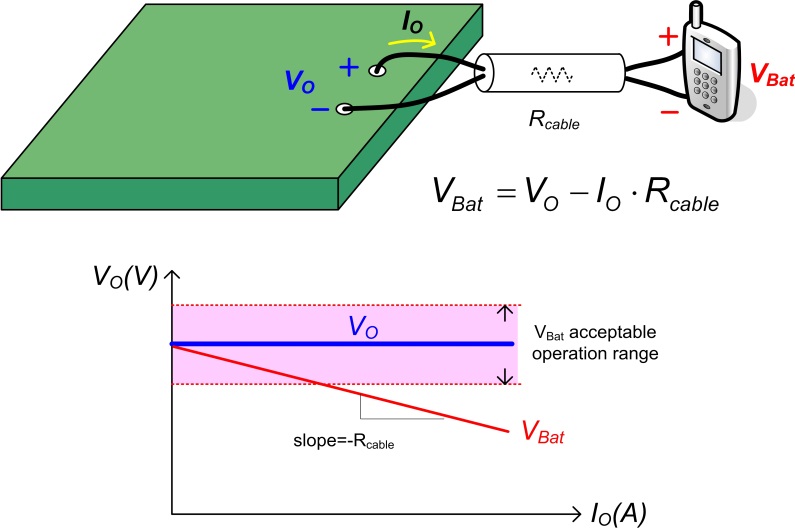
图一、缆线阻抗所造成的电压降
缆线补偿的概念,就是控制输出电压 VO
随输出电流 IO 以缆线阻抗 Rcable 线性上升,进而达到一稳定之充电电压
VBat。图二显示两种实现缆线补偿的方法,其中一种称为缆线加法补偿
(cable plus compensation),其方法是把输出电流 IO 透过一直流增益
K 形成补偿信号 K∙IO,将此补偿信号加到参考电压
VREF 上,再将结果输入至误差放大器的非反相端。所需的补偿电压可以借着补偿信号
K∙IO 准确地反映在参考电压的增量上,而直流增益K值可以由式 (1) 得到。而另一种缆线补偿方法称为缆线减法补偿
(cable minus compensation),其作法是从反饋电压 VFB 减去补偿信号
K∙IO 后,再经由阻抗 Zi 输入至误差放大器的反相端。
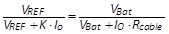 (1)
(1)
遗憾的是,PSR 方法无法直接得到二次侧输出电流讯号。但应用上为了可准确侦测二次侧输出电压讯号,反激式转换器大都是操作在不连续导通模式
(DCM, discontinuous conduction mode) 下,因此,二次侧输出电流讯号便可间接从初级侧电流讯号得到。图三是一个有缆线减法补偿的
PSR 反激式转换器之电路图。图中,补偿信号
VCC 从初级侧电流信号 IP 开始,经由电流检测电阻
RS 将初级侧电流信号IP转换成电压信号VCS,再通过一个缓冲器后形成,以此间接估计输出电流。缓冲器由一个直流增益为
KCC 的放大器和一个低通滤波器 (LPF, low pass filter) 构成,它们需要被仔细地设计。如果
LPF 的截止频率或直流增益 KCC 未作适当的设计,输出电压可能会有过补或少补的情形发生,甚至可能产生振荡的问题造成电路工作不稳定。在下一节中,我们将针对
PSR 反激式转换器的缆线补偿器和反饋控制设计进行完整详尽的小信号分析。
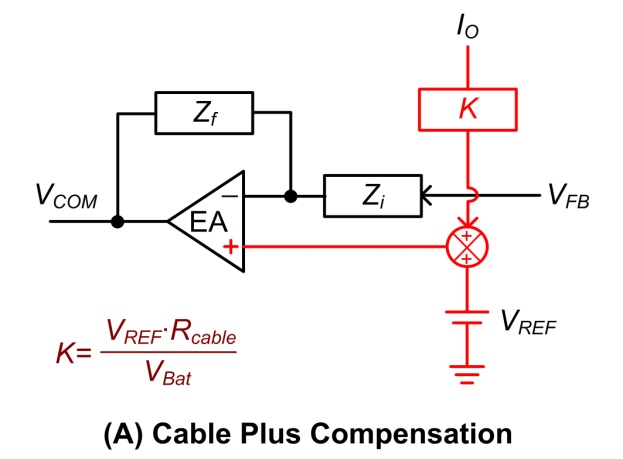
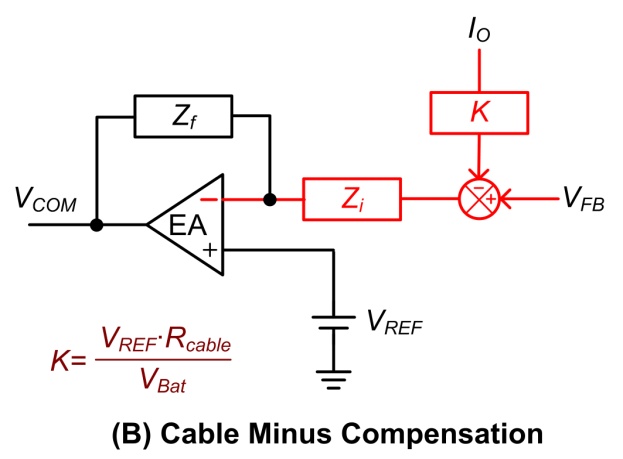
图二、缆线补偿方法: (A) 缆线加法补偿
(B) 缆线减法补偿
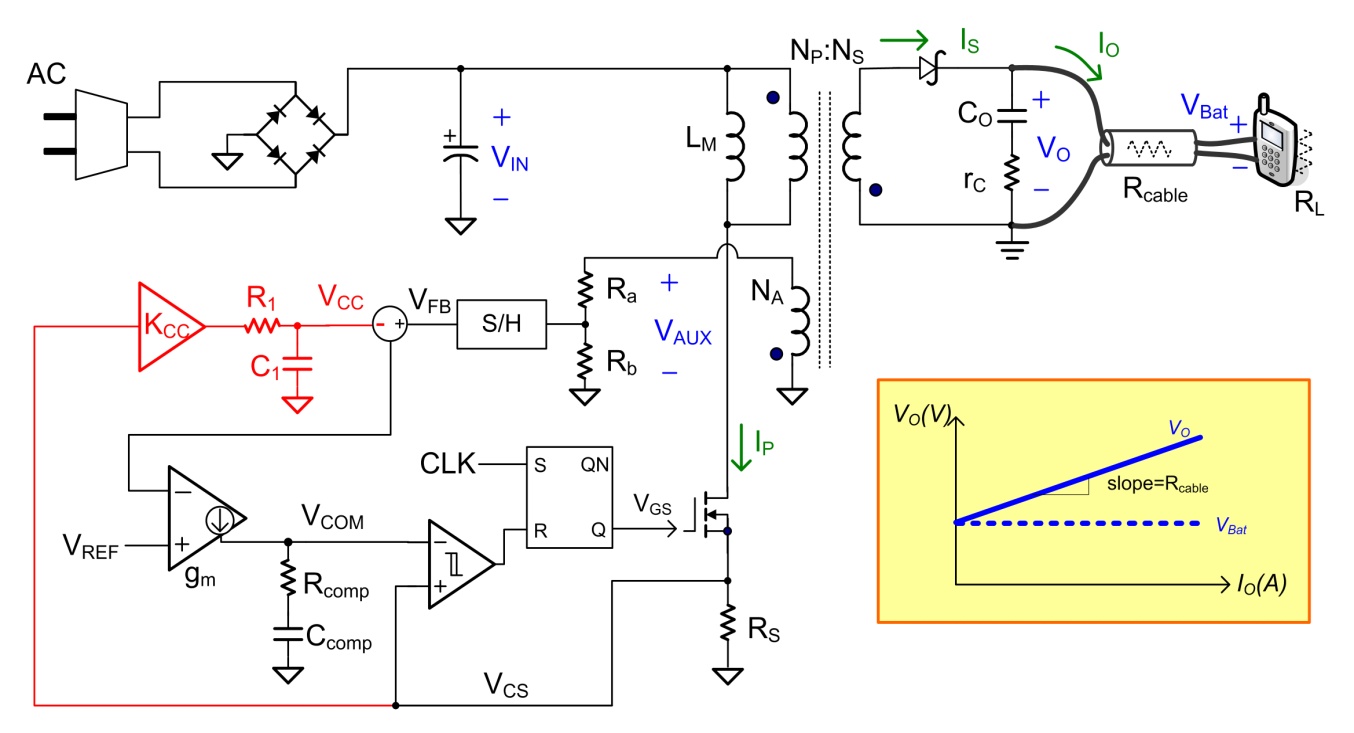
图三、有缆线减法补偿的 PSR
反激式转换器之电路图
2. 有缆线补偿的 PSR 反激式转换器的小信号分析
图四所示为一有缆线减法补偿的 PSR 反激式转换器的控制方块图。表一归纳列出在控制方块图中所用到的转换函数。从图四的控制方块图中,两个回路增益
T1 和 T2,分别代表从反馈回路中的 A 点和 B 点打断所得到的回路增益,式(2)和式(3)分别为它们的表达式,且是以电压回路增益
TV 和电流回路增益 TC 来表示的。TV 和 TC 则可分别用式(4)和式(5)表示。
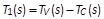 (2)
(2)
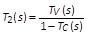 (3)
(3)
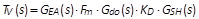 (4)
(4)
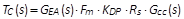 (5)
(5)
当缆线补偿参与在反馈回路时,令人惊讶的是回路增益
T2 是一个正反馈回路,即输出电压 VO
和误差放大器输出 VCOM 有相同相位。正反馈回路倾向于让系统变得不稳定,然而,借着加上负反馈回路可使系统变为稳定。回路增益
T1 则提供负反馈回路,并可用来决定系统的稳定度。当回路增益
T1 以 –20 dB/decade 的斜率通过 0 dB,并且有足够的相位裕量时,即可满足系统稳定的要求。
虽然回路增益 T2 不用于决定系统的稳定度,但它影响输出阻抗。从图四的控制方块图,输出阻抗可以由式
(6) 来表示。不同于以往的是,输出阻抗希望愈低愈好,以达到好的负载响应;但为了要提供适当的缆线补偿,反而希望输出阻抗为一负值阻抗以抵消缆线阻抗。若能将输出阻抗设计成
-Rcable,则形同缆线阻抗等效被抵消,如此充电电压便可保持稳定而不会有任何的电压降低。
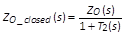 (6)
(6)
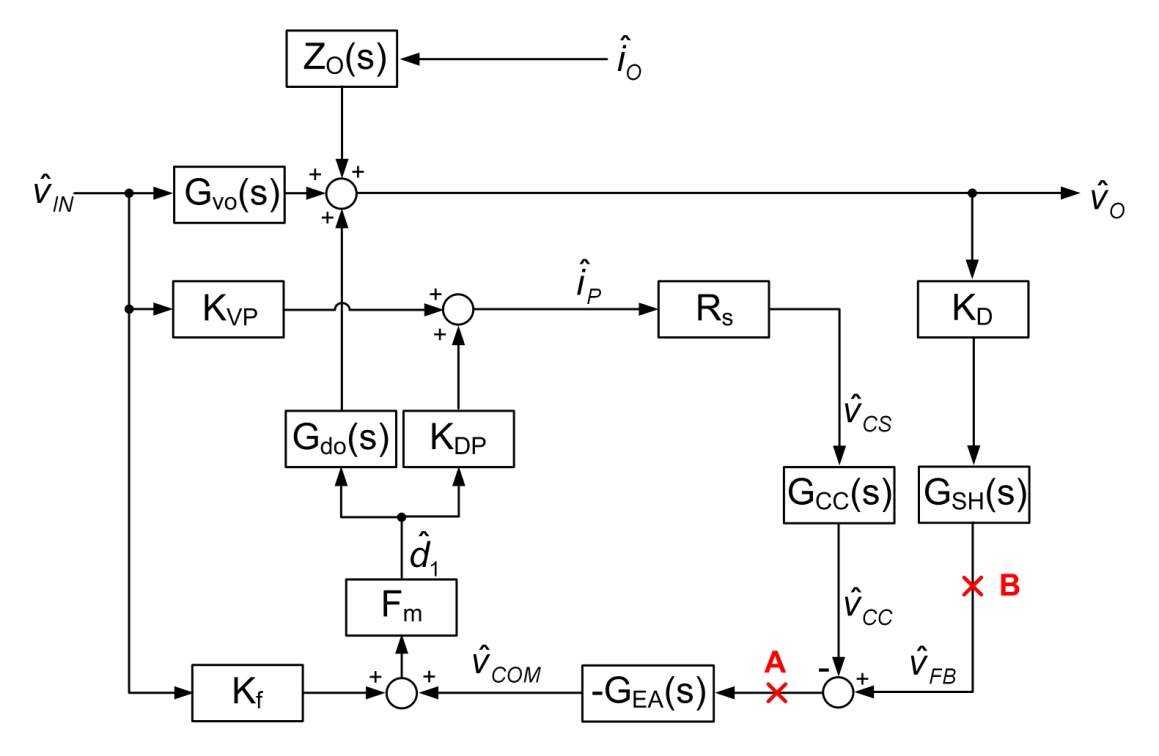
图四、有缆线减法补偿的PSR反激式转换器的控制方块图
表一、有缆线补偿的 PSR 反激式转换器之转换函数
|
Control to output
|
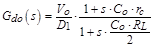
|
|
Line to output
|
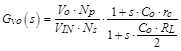
|
|
Open loop output impedance
|
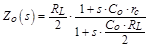
|
|
Voltage divider gain
|
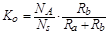
|
|
Compensator
|
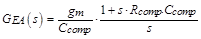
|
|
Cable compensator
|
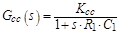
|
|
Modulation gain
|
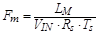
|
|
Feed forward gain
|
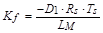
|
|
Sample & hold
|
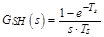
|
|
Line to primary side current gain
|
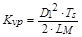
|
|
Duty to primary side current gain
|
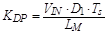
|
3. 反饋控制设计
透过从反饋电压 VFB 减去补偿信号
K∙IO 是可以有效地达成缆线补偿。然而,在 PSR 应用中,真正的补偿信号是
VCS 值经直流增益 KCC 后的平均值。由式 (7) 可得为达适当缆线补偿所需的直流增益值
KCC。较低的 KCC 值会导致输出电压补偿不足,但是较高的
KCC 值会造成输出电压补偿过度而可能导致不稳定的问题。
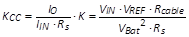 (7)
(7)
为了取得 KCC∙VCS 的平均值,低通滤波器 (LPF) 必须滤除信号中的高频部份。当
LPF 截止频率较低时,可有效衰减 KCC∙ VCS
的高频信号,可使系统较为稳定,但如此一来,便需要较大的被动元件而造成电路面积增大,在实际芯片电路设计上,并不是很好的选择。因此,截止频率的选择就必须在元件大小及系统效能上作适当取舍。
补偿器的设计目标是找到适当的补偿器增益
GEA,好使回路增益 T1 在所指定的相位裕量下能满足带宽的要求。补偿器的设计可根据
(8) 和 (9) 式进行。当 Gdo∙KD 的幅度大于 KDP∙RS∙GCC
的幅度时,Gd 就近似于 Gdo∙KD,而 Gdo∙KD
的转移函数有一个随负载变动的极点和一个左半平面的零点。用传统的电压模式控制,补偿器可以设计成一个极点在原点,另外有一个零点来补偿系统的极点,使得最后的回路增益
T1 以 –20 dB/decade 的斜率通过 0dB,达到足够的相位裕量即可使得系统可以稳定。
然而,如果 KDP∙RS∙GCC 和 Gdo∙KD
的幅度很接近时,Gd 会变成有两个极点和两个零点的转移函数,其关系式如式
(9) 所示。若 LPF 的截止频率如图五所示逐渐增加,当截止频率超过某一频率时,KDP∙RS∙GCC
的幅度开始大于 Gdo∙KD,这时Gd两个左半平面的零点便会移至右半平面,系统则会趋于不稳定。所以,根据上述分析,设计者可先假设
KDP∙RS∙GCC 的幅度小于 Gdo∙KD
的幅度,用式 (8) 来设计补偿器,之后再设计
LPF 的截止频率,让 KDP∙RS∙GCC
的幅度永远小于 Gdo∙KD,如此系统就可以达到稳定的状态。
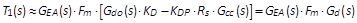 (8)
(8)
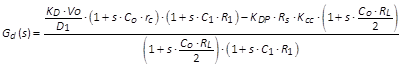 (9)
(9)
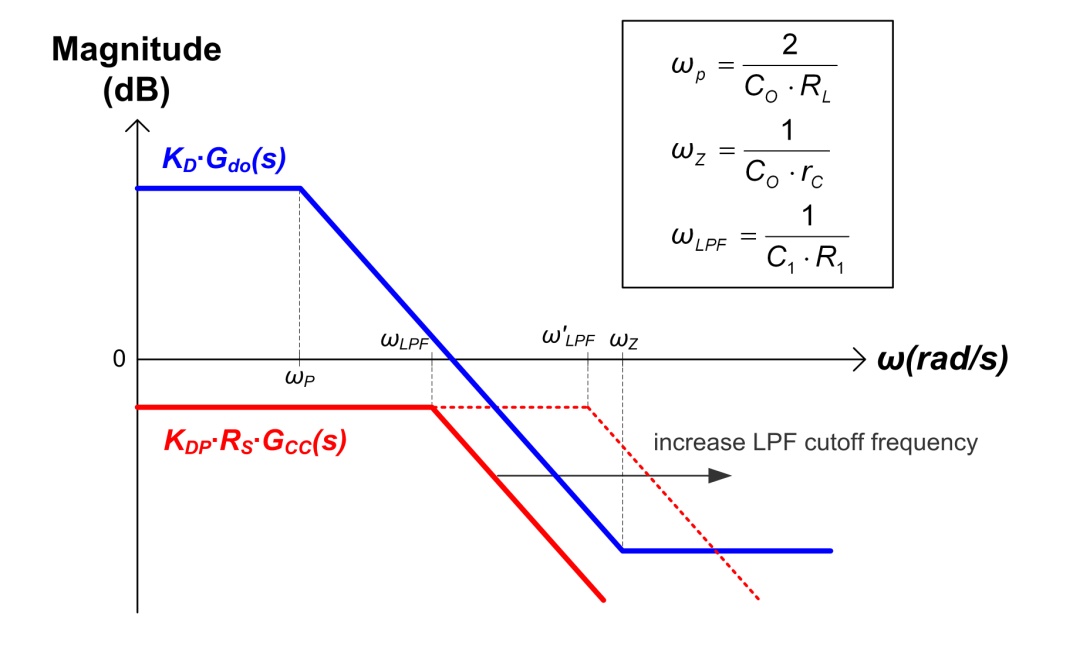
图五、KDP∙RS∙GCC
和 Gdo∙KD 的曲线图
4. 电路仿真验证
以电路仿真来验证理论分析结果,所用参数列于下。VIN
= 156V,VBat = 5V,IO = 1A,LM = 1.5mH,CO
= 1mF,rC = 20mΩ,RS = 4.5Ω,Rcable = 240mΩ,NP
: NS : NA = 15 : 1 : 1.4,fS = 50kHz,VREF
= 1.2V,gm = 100μA/V,Rcomp = 215kΩ,Ccomp = 12nF,Ra
= 29kΩ,Rb = 6kΩ,R1 = 100kΩ,C1 = 5nF 且 KCC
= 400m。图六同时显示有缆线补偿和没有缆线补偿的模拟波形图,在不同的负载条件下,缆线补偿都适当地提供一稳定之充电电压。图七和图八分别显示回路增益
T1 和 T2。由图可知,电路仿真结果与分析计算结果非常吻合,系统的带宽和相位裕量是由回路增益
T1 决定,且由图八可知回路增益 T2 是正反饋。图九显示的是输出阻抗,它在低频的增益接近于
Rcable,不过相位是从 180° 开始,也就是它提供了负阻抗以有效抵消缆线阻抗。
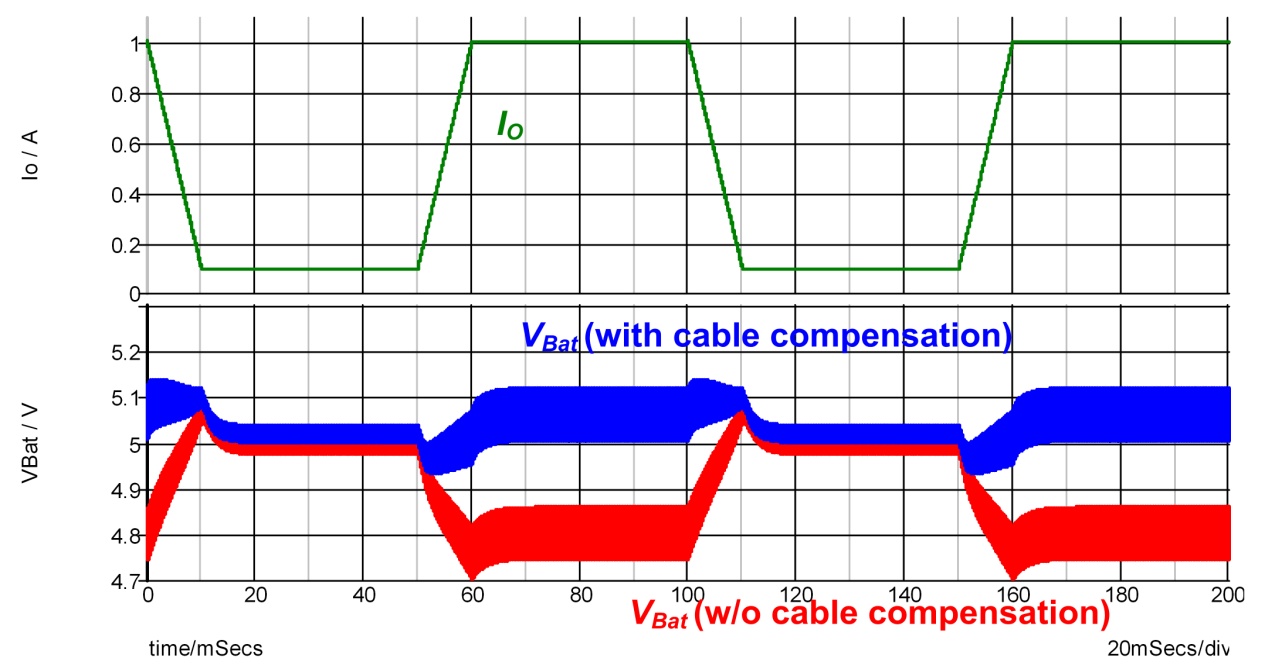
图六、有缆线补偿和没有缆线补偿的模拟波形图
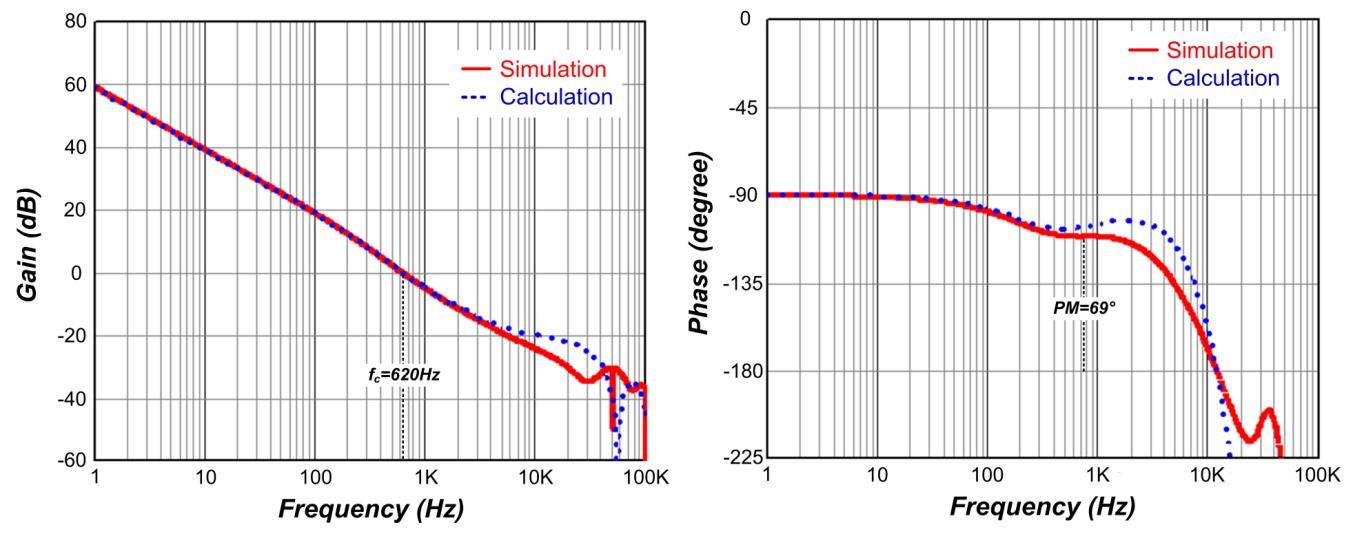
图七、回路增益 T1 的波德图
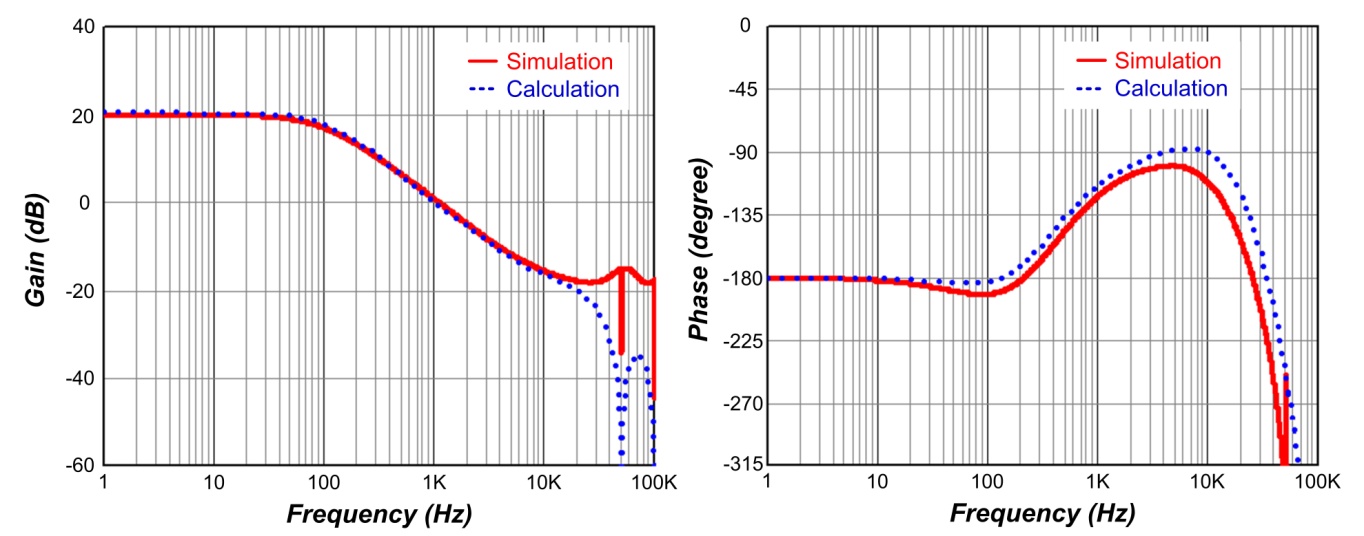
图八、回路增益 T2 的波德图
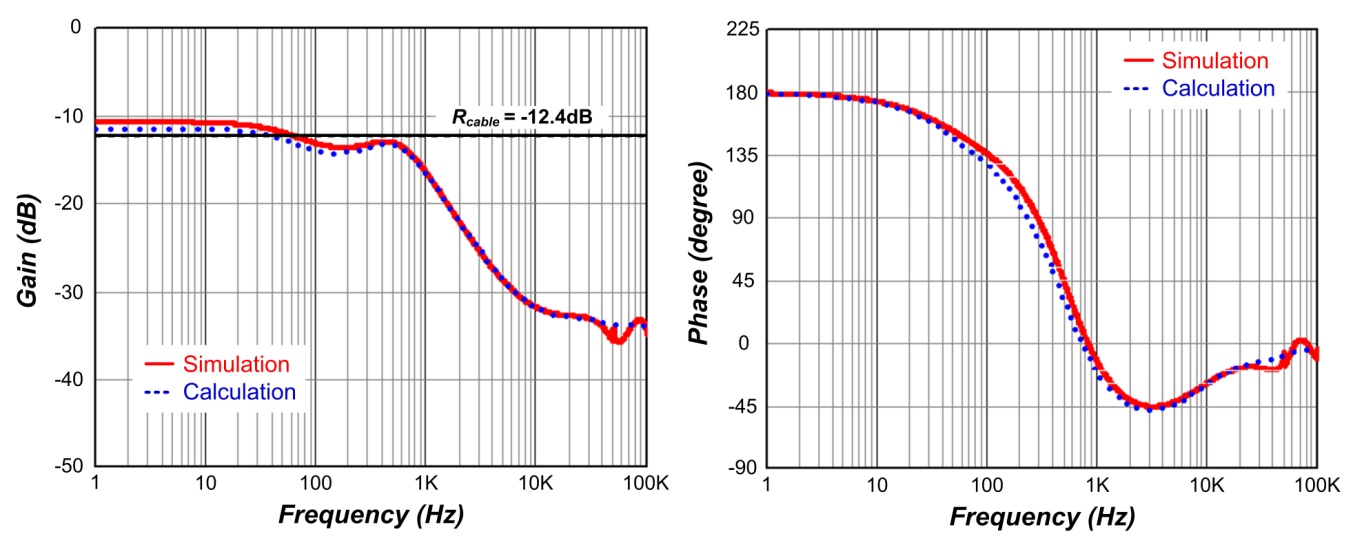
图九、输出阻抗的波德图
图十显示分别在不同的 C1 值而产生不同的 LPF 截止频率之下,输出电压仿真波形与回路增益
T1 的计算结果。从结果发现,C1
容值小而让 LPF 截止频率变高会造成系统不稳定,而根据前面回路增益
T1 的分析结果,此不稳定的现象也可从其增益余量或相位余量得到预测。所以,当
R1 恒定时,可由 KDP∙RS∙GCC
和 Gdo∙KD 的波德图来决定让系统稳定的最小电容
C1。图十一显示 KDP∙RS∙GCC
和 Gdo∙KD 的波德图在不同 C1 状况下的表现,由该图可发现
C1 至少须大于 3nF 才能使得 KDP∙RS∙GCC
永远小于Gdo∙KD。经过电路仿真可知让系统稳定的最小
C1 值为 4nF,这验证了上述分析的结果。
图十二显示在各个不同 C1 值时,回路增益 T1
的带宽和相位裕量图形。由图可知,当 C1 值较大时,系统会有较高的带宽与相位裕量;但是,当
C1 超过某一定值后,系统效能无法再有显著的改善,只是付出不必要的成本而已。由此可知,本文所提出的小信号分析方法,能为反饋设计提供有效的帮助。
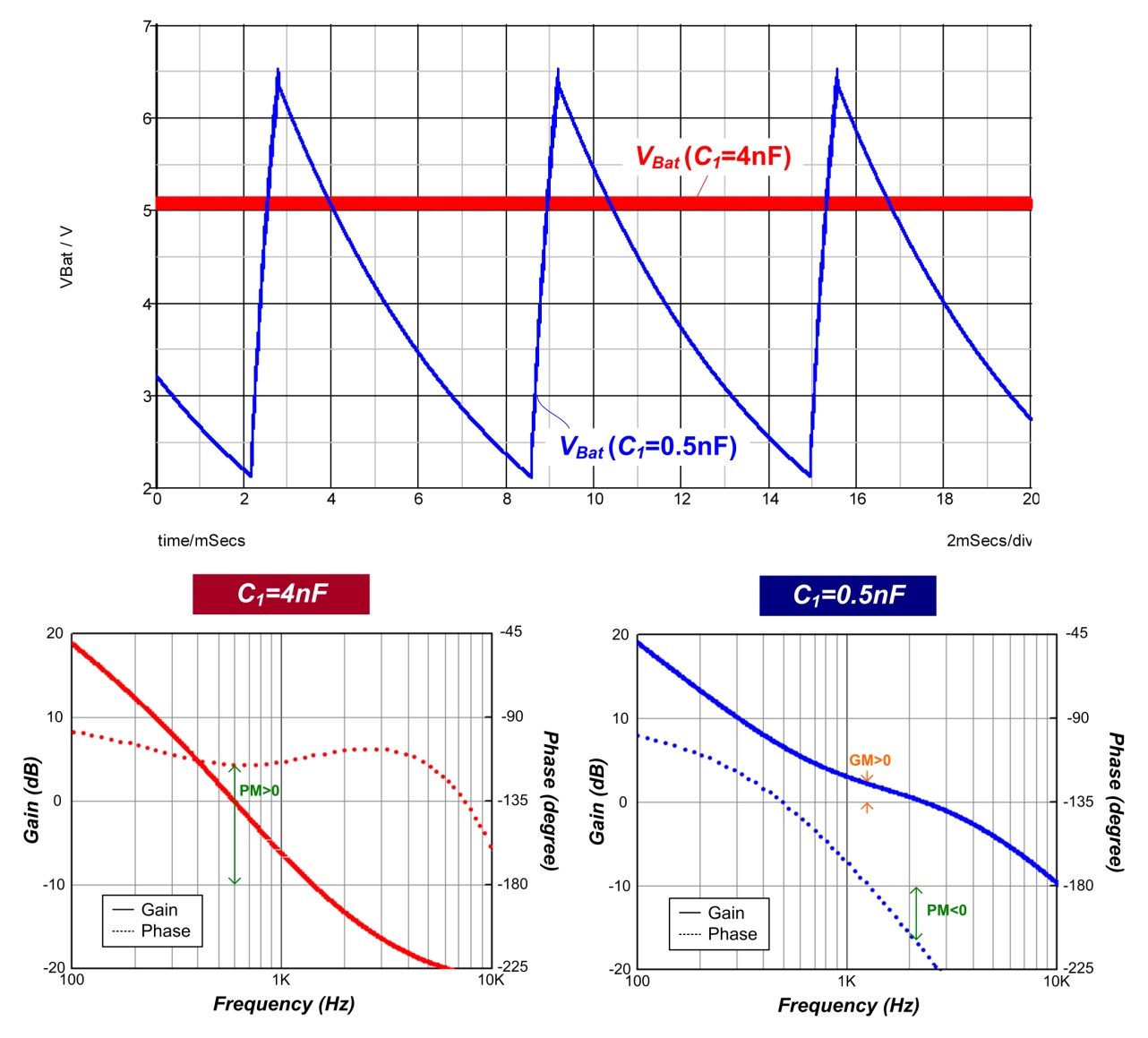
图十、在不同 C1 值下,充电电压
VBat 的电路仿真波形图和回路增益 T1 的计算结果。
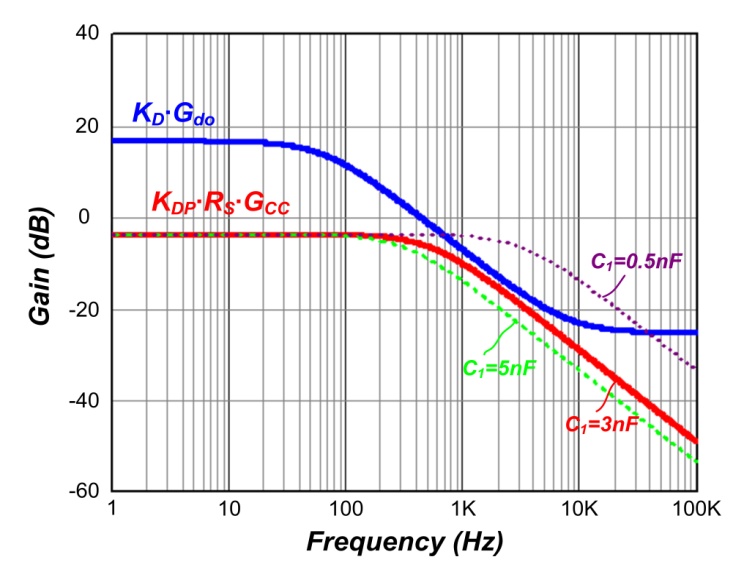
图十一、不同 C1 值时 KDP∙RS∙GCC
和 Gdo∙KD 的图形
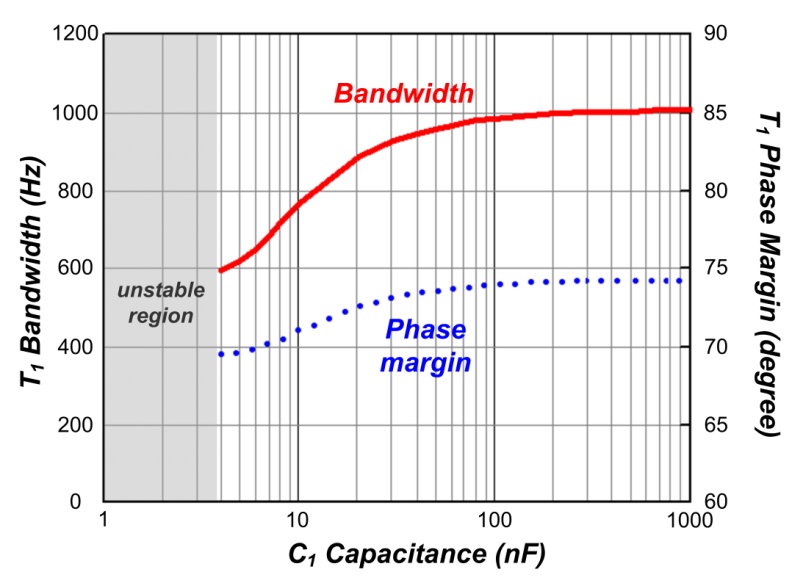
图十二、不同 C1 值下,回路增益 T1 的带宽与相位裕量的图形
5. 总结
本文提出了一个应用在 PSR 反激式转换器上的缆线补偿方式以解决在电池充电器应用中的因缆线阻抗所造成的电压降问题,其中提出的小信号模型为进行缆线补偿设计提供了小信号分析及反饋控制设计的完整而详尽的工具,而分析的结果,也经由电路仿真得到有效的验证。